Когерентный демодулятор

Это третья статья из цикла статей про мои программы для цифровой обработки сигналов (ЦОС). С выделением стволов из группового спектра разобрались. С определением параметров сигнала тоже. Теперь можно рассказать о демодуляторе. Тема демодуляции очень объемна и заслуживает не одной книги. Я постараюсь вкратце изложить архитектуру демодулятора и назначение основных блоков. Надеюсь, что для кого то эта статья станет хорошей отправной точкой.

Исходные данные:

1. Файл оцифрованных сигналов с выхода приемника в широкой полосе частот. Например у вас есть АЦП с частотой дискретизации равной 200 МГц. С помощью такого АЦП вы можете оцифровать сигналы в полосе до 100 МГц. Затем в отложенном режиме проанализировать и демодулировать все сигналы находящиеся в этом файле.

2. Параметры сигнала полученные в результате предварительного анализа:

• частота дискретизации АЦП
• разрядность АЦП
• несущая частота
• тактовая частота
• вид модуляции

Структурная схема квадратурного демодулятора

Частота дискретизации сигнала в АЦП не кратна тактовой частоте сигнала и в оцифрованном файле может быть больше чем один сигнал (до 300). По этим причинам структурная схема демодулятора имеет вид, приведенный на рис. 1.

Рис. 1. Структурная схема когерентного демодулятора

Назначение, состав, принцип работы составных модулей

1. Модуль чтения из файла. Здесь все просто. Например в файле хранятся 16-ти битные отсчеты АЦП. Демодулятор работает с числами двойной точности (double). Модуль предназначен для чтения отсчетов АЦП из файла и преобразование их в double формат. Следует заметить, что есть тут одна тонкость. Следующим модулем является FFT фильтр в котором используется быстрое преобразование Фурье для работы которого необходимо, чтобы размер обрабатываемых блоков был кратен степени 2. Например 218 = 262144 отсчетов АЦП.

2. FFT фильтр. Как я уже говорил в файле хранятся сигналы в некоторой полосе частот. Таких сигналов в файле может быть очень много. Для дальнейшей работы с сигналом необходимо его сначала “вырезать“ удалив все ненужные сигналы. Лучше всего для этого подходит фильтрация в частотной области. Если очень по простому то операция фильтрации состоит из 3-х частей:
— Выполняется прямое преобразование Фурье для получение спектра сигнала;
— Обнуление в спектре сигнала лишних частот. Так как мы знаем несущую частоту и ширину спектра сигнала это не представляет трудов;
— Выполняется обратное преобразование Фурье.

В итоге мы получаем отфильтрованный сигнал. Это если по простому, но есть несколько тонкостей. Дело в том, что так как мы имеем дело не с бесконечным сигналом, а с блоками конечной длины, то на краях блока возникают искажения сигнала. Для того чтобы избавиться от искажений, необходимо производить фильтрацию блоков с перекрытием (внахлест). Более детально об этом можете почитать в статье FFT анализ где автор “на пальцах” рассказывает об FFT фильтрации.

3. Формирователь квадратур. Задача этого модуля очень проста как и его реализация — это перенос спектра сигнала на нулевую частоту и формирование квадратурных составляющих I и Q. Надо понимать, что на вход блока подается отфильтрованный сигнал. Математически выглядит все очень сложно. Кому интересно можете прочитать в книге «Цифровая связь» автор Прокис Дж. стр. 287 внизу страницы начиная со слов “Сигнал КАМ и многопозиционный ФМ можно представить так”.

Если своими словами то на передающей стороне спектр сигнала формировался из 2-х квадратурных составляющих I и Q, а наша задача на приемной стороне получить их. Делается это очень просто. Сначала высокочастотный сигнал умножается на несущую с частотой равной несущей сигнала. Что происходит при умножении? Гармонические составляющие двух сигналов складываются, вычитаются и т.д. Нам интересно их вычитание. Если принять, что частоты умножаемых сигналов равны, то при вычитании получается 0. Таким образом мы получаем перенос спектра сигнала в 0. При умножении получается куча других гармонических составляющих которые нам не нужны. Как от них избавиться будет описано ниже. Так мы получили первую квадратурную составляющую. Чтобы получить вторую необходимо тот же высокочастотный сигнал умножить на несущую , но теперь сдвинутую по фазе на 90°.

4. Коммутатор. В статье на рисунке 7 представлена схема частного случая когерентного демодулятора когда частота дискретизации сигнала в АЦП берется кратной тактовой частоте сигнала: fд = 2ifт, где i = 2,3,4,… В моем случае такая схема не подходила потому как тактовая частота сигналов в оцифрованном сигнале может быть разной. В этих случаях используется схема приведенная в той же статье на рисунке 8.

В моем случае эта схема претерпела изменение и пришлось добавлять коммутатор. Дело в том, что разброс тактовых частот сигналов на столько велик, что в некоторых случаях необходимо производить децимацию сигнала в других интерполяцию. В зависимости от значения тактовой частоты выбирается одна из двух цепей обработки.

5. Приведение частоты дискретизации к 10*Ft. На данном этапе обработки сигнала существует 2 проблемы. Первая проблема — это то, что в формирователе квадратур при умножении получается куча паразитных гармонических составляющих. От них можно просто избавиться с помощью фильтра нижних частот (ФНЧ). Вторая проблема — это то, что тактовая частота сигнала не кратна частоте дискретизации. Эта проблема решается с помощью блоков децимации и интерполяции.

Моей задачей было разработать схему которая решает обе задачи сразу так как они тесно связаны друг с другом. Дело в том, что децимация не возможна без низкочастотной фильтрации.

Пару слов про децимацию. Нельзя просто так выбросить (удалить) лишние отсчеты из сигнала.

Рис. 2. Главное правило децимации

Казалось вроде все просто. Если надо уменьшить частоту дискретизации вдвое, то просто удаляешь отчеты через один. Если втрое, то оставляешь каждый третий отсчет и т.д. Но не тут то было. Для осуществления децимации необходимо выполнить условие, чтобы исходный сигнал не содержал частоты, превышающие частоту Найквиста децимированного сигнала, иначе при децимации будет иметь место алиасинг (наложение спектров).

Например, есть сигнал с частотой дискретизации 10 МГц, тогда частота Найквиста будет равна 5 МГц (Рисунок 3 п. а). Предположим, что нам необходимо произвести децимацию в 2 раза. В этом случае новая частота дискретизации будет равна 10 / 2 = 5 МГц, а новая частота Найквиста будет равна половине новой частоты дискретизации 5 / 2 = 2.5 МГц (Рисунок 3 п. б). Таким образом для того , чтобы не внести искажения в сигнал связанные с алиасингом необходимо перед процедурой прореживания (удаления) произвести низкочастотную фильтрацию фильтром полоса пропускания которого должна быть меньше новой частоты Найквиста (Рисунок 3 п. в).

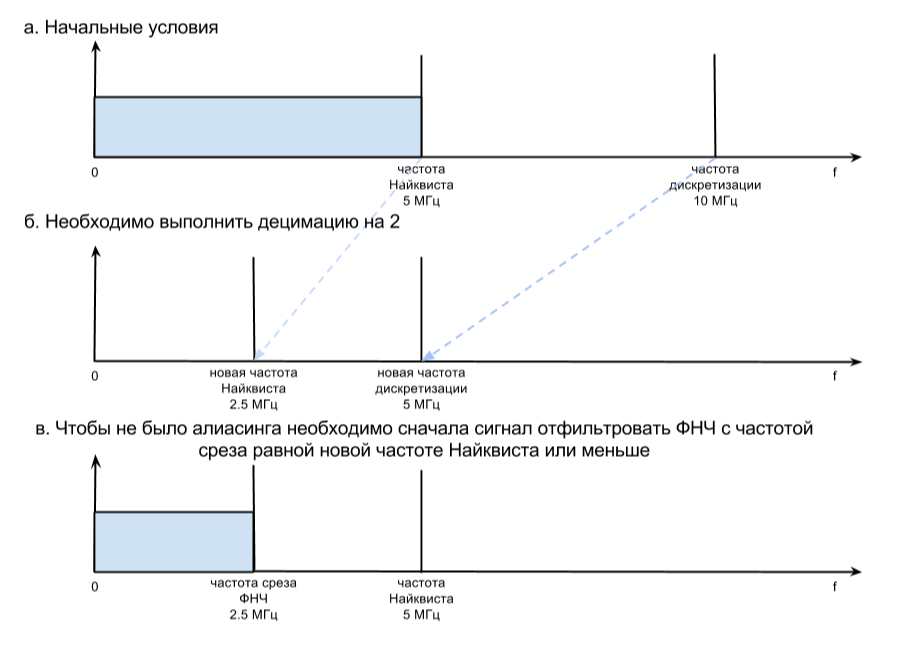Рис. 3. Пример децимации в 2 раза

С фильтрацией побочных гармоник вроде разобрались.

Второй не решенной задачей является то, что частота дискретизации не кратна тактовой частоте и количество отсчетов АЦП на такт величина не постоянная.  Если решить эти проблемы то дальнейшая схема демодулятора станет универсальной и не будет зависеть от тактовой частоты сигнала. В результате исследований я пришел к тому, что для дальнейшей обработки сигнала достаточно 10 отсчетов на такт.

Рассмотрим теперь подробней левую часть блока. Мы видим, что применяется 2-х каскада децимации. Сделано это потому, что если тактовая частота сигнала маленькая, то коэффициент децимации становится на столько большим, а частота Найквиста на столько низкой, что трудно реализовать ФНЧ. Например при частоте дискретизации 200 МГц и тактовой частоте сигнала 20 КГц мы имеем 200 МГц / 20 КГц = 10000 отсчетов на такт. Делим полученное число на 10 так как на выходе хотим получить фиксированную частоту дискретизации 10*Ft. Получаем величину 10000 / 10 = 1000. В этом случае нам необходимо произвести децимацию в 1000! раз.

Для решения этой проблемы была разработана схема поэтапной децимации из 2-х каскадов. При таком подходе коэффициенты децимации каскадов умножаются. То есть чтобы реализовать децимацию в 1000 раз достаточно 2-х каскадов с децимацией 25 и 40.  В случае если коэффициент децимации не большой то используется только один каскад. Коэффициенты децимации подбираются таким образом чтобы максимально приблизить итоговую частоту дискретизации к 10*Ft.

6. Модули работающие на частоте 10*Ft. Начиная с этого этапа все модули демодулятора работают в одинаковых условиях вне зависимости от начальных условий. Это очень удобно для отладки и позволяет использовать следующие модули для различных решений. По сути до этого были подготовительные этапы. Теперь начинается демодуляция. Такое решение удобно еще и тем, что предыдущие этапы можно отбросить если иметь комплексные отсчёты оцифрованного сигнала с частотой дискретизации равной 10*Ft. То есть можно применить схему демодуляции когда фильтрация сигнала, формирование квадратур и децимация выполняется аппаратно. Такое решение на порядки увеличит скорость демодуляции.

Почему именно 10*Ft? Цифра 10 получена в результате экспериментов. Мне хотелось повысить качество работы фазовращателя и согласованного фильтра, но при этом не очень потерять в скорости обработки.

7. Усилитель. Выполняет операцию умножения отсчетов сигнала на величину полученную с выхода системы автоматической регулировки усиления (САРУ).

8. Фазовращатель. При определении параметров сигнала мы получили ошибку определения несущей частоты и ошибку начальной фазы. Ошибка определения частоты сигнала приводит к тому, что на сигнальном созвездии точки постоянно вращаются. Направление вращения (по часовой или против) зависит от знака ошибки. Допустим мы без ошибки определили частоту сигнала или устранили ошибку, но мы не знаем начальную фазу сигнала. Ошибка определения начальной фазы приводит к тому что сигнальное созвездие будет наклонено на угол равный ошибке определения. Модуль фазовращателя устраняет эти ошибки. Его задача не допустить вращение и наклон сигнального созвездия. Фазовращатель работает постоянно так как несущая частота сигнала может быть величиной не постоянной.

9. Согласованный фильтр. При передаче сигналов всегда идет борьба между скоростью передачи и шириной спектра сигнала. Дело в том что чем выше скорость передачи тем шире спектр сигнала. В системах передачи данных от ширины спектра сигнала зависит стоимость оказываемой услуги. Есть еще одна сторона вопроса. По цифровым каналам связи сигналы передаются прямоугольными импульсами. Прямоугольный импульс имеет бесконечный спектр. Крайний случай передачи данных это когда передаются последовательно  «0» и «1» (меандр). Спектр меандра пропорционален функции sinc(x).

Для уменьшения ширины спектра на передающей стороне сигнал фильтруется для удаления высокочастотных составляющих, но в результате фильтрации происходит межсимвольная интерференция. Если знать закон (правило) фильтрации, то на приемной стороне можно произвести обратное преобразование которое позволит устранить пагубное влияние межсимвольной интерференции. Этой задачей и занимается согласованный фильтр.

10. Дециматор на 5. Приводит частоту дисктеризации 10*Ft к 2*Ft. Таким образом коэффициент децимации давен 5.

11. Модули работающие на частоте 2*Ft. Начиная с этого этапа все модули демодулятора работают на скорости 2*Ft (удвоенной тактовой). 2*Ft — это минимальная частота на которой могут работать адаптивный корректор и решающее устройство.

12. Адаптивный корректор. В результате прохождения сигнала через атмосферу или например за счет переотражения сигнала от зданий на него накладываются нелинейные помехи характеристика которых тесно связана с характеристикой канала передачи данных. Целью адаптивного корректора является вычисление характеристики канала передачи данных и устранение его влияния на качество сигнала.

13. Принятие решения. Соль демодулятора. Именно тут принимается решение по принятой точке на сигнальном созвездии. Принятая точка «притягивается» к эталонной по критерию минимального расстояния. По двум точкам на плоскости (принятой и эталонной) вычисляются ошибки для системы автоматической регулировки усиления, системы восстановления несущей и системы восстановления тактовой.

14. Петли обратной связи. Для усилителя (7) система автоматической регулировки усиления (САРУ) вычисляет коэффициент на который необходимо умножить сигнал для того чтобы он полностью помещался с сигнальное созвездие. Для фазовращателя (8) система восстановления несущей (СВН) вычисляет ошибку определения несущей частоты и её начальной фазы. Для блоков децимации (5) система тактовой синхронизации вычисляется ошибку определения тактовой частоты и её начальной фазы.

Вот вроде и все. Получилось даже больше чем планировал. Очень надеюсь, что кому то пригодятся мои знания.